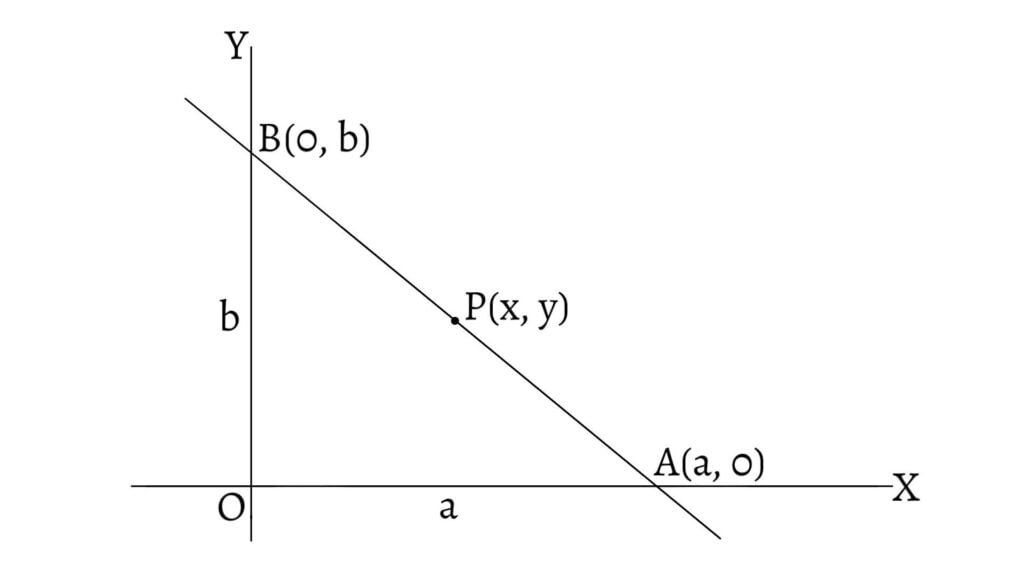
Here, we will discuss about the double intercept form of the equation of straight lines.
Let a straight line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively. Then, the intercepts on the x-axis and y-axis are $OA=a$ and $OB=b$ respectively. Also, let $P(x,y)$ be any point on $AB$.

This is the equation of the line whose intercepts are $a$ and $b$ and is known as the double intercept form. This form of the equation of a straight line cannot be used if the line passes through the origin or if it be parallel to any one of the axes.
Since this line passes through the point $(3,4)$, \[3+4=a\] \[\therefore a=7\]
Putting the value of $a$ in $\text$, \[x+y=7\] which is the required equation of the line.
Solving $\text$ and $\text$, \[3(14-a)+4a=a(14-a)\] \[42-3a+4a=14a-a^2\] \[a^2-13a+42=0\] \[(a-6)(a-7)=0\] \[\therefore a=6,7\]
Taking $a=6$, $b=14-6=8$. Then, the required equation of the line is \[\frac+\frac=1\] \[\therefore 4x+3y=24\]
Taking $a=7$, $b=14-7=7$. Then, the required equation of the line is, \[\frac+\frac=1\] \[\therefore x+y=7\]
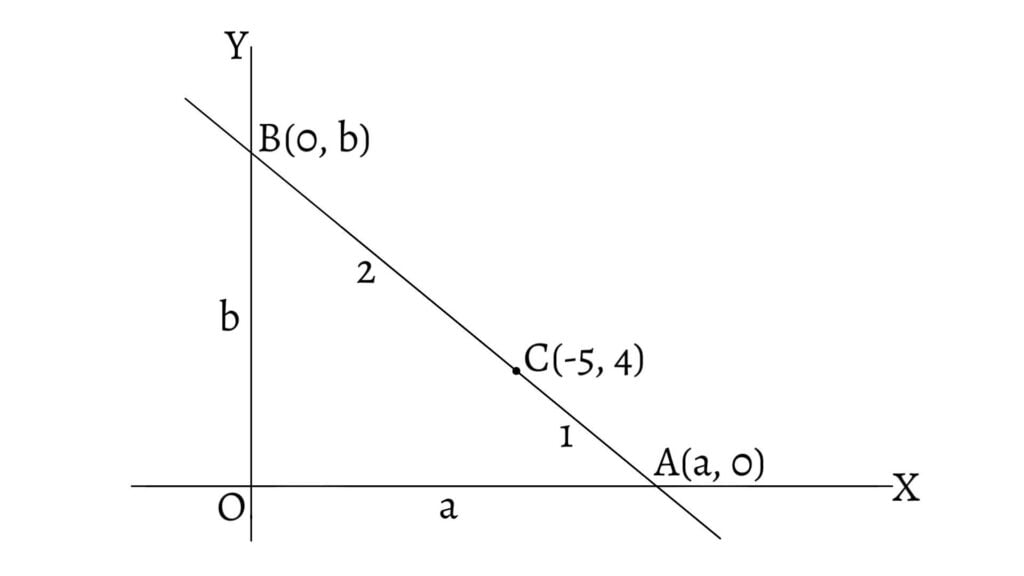 in the ratio 1:2" width="1024" height="576" />
in the ratio 1:2" width="1024" height="576" />
Let the line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively and $AB$ is divided at $C$ in the ratio $1:2$. Then, from section formula for internal division, we have, \[-5=\frac\text< and >4=\frac\] \[-5=\frac\text< and >4=\frac\] \[\therefore a=\frac\text< and >b=12\]